230221 소프트웨어 개발 : 자료 구조

트리 : Node와  Branch를 이용하여, 사이클을 이루지 않도록 구성한 데이터 구조

기본 용어

• Node
• Root Node
• Level
• Parent Node
• Child Node
• Leaf Node (Terminal Node)
• Sibling
• Depth

• 노드의 크기(size) : 자신을 포함한 모든 자손 노드의 개수.
  • C의 크기 : 6
• 노드의 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
  • D의 깊이 : 2
  • L의 깊이 : 3
• 노드의 레벨(level) : 트리의 특정 깊이를 가지는 노드의 집합
  • A의 레벨 : 1
  • B, C의 레벨 : 2
  • D, E, F, G, H의 레벨 : 3
• 노드의 차수(degree) : 부(하위) 트리 갯수/간선수 (degree) = 각 노드가 지닌 가지의 수
  • A의 차수 = 2
  • B의 차수 = 3
  • C의 차수 = 2
• 트리의 차수(degree of tree) : 트리의 최대 차수
  • B가 최대 차수를 가짐 => 3
• 트리의 높이(height) : 루트 노드에서 가장 깊숙히 있는 노드의 깊이
  • 3

트리의 기본 성질

• 노드가 N개인 트리는 항상 N-1개의 링크(link)를 가진다
• 트리에서, 루트에서 어떤 노드로 가는 경로는 유일하다. 또한 임의의 두 노드 간의 경로도 유일하다 (같은 노드를 두 번 이상 방문하지 않는 다는 조건 하에)

Pre order

Pre Order의 방문 순서는 다음과 같습니다.

노드 방문 -> 왼쪽 서브 트리의 프리오더 -> 오른쪽 서브 트리의 프리오더 

 

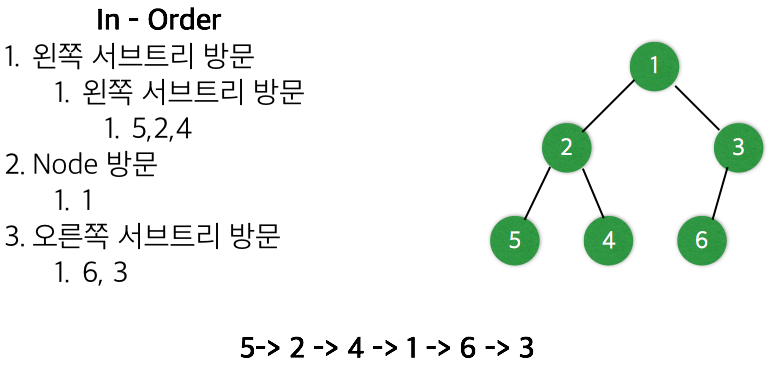
In Order

In Order의 방문 순서는 다음과 같습니다.

왼쪽 서브 트리의 프리오더 -> 노드 방문 -> 오른쪽 서브 트리의 프리오더 

 

Post Order(전위 순회)

Post Order의 방문 순서는 다음과 같습니다.

왼쪽 서브 트리의 프리오더 -> 오른쪽 서브 트리의 프리오더 -> 노드 방문  

출처: https://manducku.tistory.com/34 [Manducku`s Code]

 

- 산술을 계산하기 위해 기억공간에 기억시키는 방법으로 이진 트리를 많이 사용한다. 이진 트리로 만들어진 수식을 인오더, 프리오더, 포스트오더로 운행하면 각각 중위(Infix), 전위(Prefix), 후위(Postfix) 표기법이 된다.

- 전위 표기법(PreFix) : 연산자 -> Left -> Right (+AB)

- 중위 표기법(InFix) : Left -> 연산자 -> Right (A+B)

- 후위 표기법(PostFix) : Left -> Right -> 연산자 (AB+)

 

1) Infix 표기를 Prefix로 변환하기

X = A / B * (C + D) + E

(X = (((A / B) * (C + D))+E)) : 연산 우선순위에 따라 괄호로 묶는다.

=(X+(*(/(A B)+(C D))E)) : 연산자를 해당 괄호 앞으로 옮긴다.

=X+*/AB+CDE : 필요없는 괄호를 제거한다

 

2) Infix 표기를 Postfix로 변환하기

X = A / B * (C + D) + E

(X = (((A / B) * (C + D))+E)) : 연산 우선순위에 따라 괄호로 묶는다.

(X(((A B)/(C D)+)*E)+)= : 연산자를 해당 괄호의 뒤로 옮긴다.

XAB/CD+*E+= : 필요없는 괄호를 제거한다.

 

3) Postfix 표기를 Infix로 변환하기

A B C - / D E F + * +

((A (B C -) /) (D (E F +) *) +) : 먼저 인접한 피연산자 두 개와 오른쪽 연산자를 괄호로 묶는다.

((A / (B - C)) + (D * (E + F))) : 연산자를 해당 피연산자의 가운데로 이동시킨다

A / (B - C) + D * (E + F) : 필요 없는 괄호를 제거한다.

 

4) Prefix 표기를 Infix로 변환하기

+ / A - B C * D + E F

(+ (/ A (- B C)) (* D (+ E F))) : 먼저 인접한 피연산자 두 개와 왼쪽 연산자를 괄호로 묶는다.

((A / (B - C)) + (D * (E + F))) : 연산자를 해당 피연산자의 가운데로 이동시킨다

A / (B - C) + D * (E + F) : 필요 없는 괄호를 제거한다.

 

출처: jess2.tistory.com/63

그래프란 ? 

그래프는 정점(Vertex)간의 관계를 표현하는 자료구조 입니다. 

그래프 G = (V,E)로 정의하는데, V(Vertex)는 그래프에 있는 정점들의 집합을 의미하고 E(Edge)는 정점을 연결하는 간선들의 집합을 의미합니다.

 

사실 일상생활에서 그래프의 개념은 많이 사용되고 있습니다. 그 중에 가장 대표적인 것이 지하철노선도 인데요, 각 지하철역과 그 들을 연결하는 호선간의 관계를 그래프로 표현할 수 있습니다.

 

그래프와 트리의 차이

 

출처 : https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html

무방향 그래프(Undirected Graph)

무방향 그래프는 두 정점을 연결하는 간선에 방향이 없는 그래프이다. 정점 v1와 v2를 연결하는 간선을 [v1, v2]라고 하면, 이때 [v1, v2]와 [v2, v1]은 같은 간선이다. 

출처 : https://www.zerocho.com/category/Algorithm/post/584b9033580277001862f16c

 

방향 그래프(Directed Graph)

방향 그래프는 다이그래프(digraph)라고도 하는데, 간선에 방향이 있는 그래프이다. 정점 v1와 v2를 연결하는 간선을 [v1, v2]라고 하면, 이때 [v1, v2]와 [v2, v1]은 같을 수 없다, [v1, v2]는 정점 v1에서 v2로만 갈 수 있는 간선을 의미한다.

출처 : https://www.zerocho.com/category/Algorithm/post/584b9033580277001862f16c

 

완전 그래프(Complete Graph)

완전 그래프는 한 정점에서 모든 다른 정점과 연결되어 최대의 간선수를 가지는 그래프다.

     무방향 그래프에서의 최대 간선 수 : n(n-1)/2

        방향 그래프에서의 최대 간선 수 : n(n-1)/1

출처 : https://itdexter.tistory.com/84

 

부분 그래프(subgraph)

원래의 그래프에서 일부의 정점이나 간선을 제외하여 만든 그래프를 의미한다.

 

출처 : https://itdexter.tistory.com/84

 

가중 그래프(Weight Graph)

정점을 연결하는 간선에 가중치를 할당한 그래프를 의미한다.

출처 : https://itdexter.tistory.com/84

 

그래프 용어

정점(Vertex) : 연결한 객체들을 의미

간선(Edge) : 정점들을 연결하는 선

차수(Degree) : 정점에 연결되어 있는 간선의 수, 방향 그래프에서 진입/진출 차수의 합

진입차수(In-Degree) : 방향 그래프에서 정점을 머리로 하는 간선의 수, 정점으로 들어오는 간선

진출차수(Out-Degree) : 방향 그래프에서 정점을 꼬리로 하는 건선의 수, 정점에서 나가는 간선

경로(Path) : 정점A에서 정점B까지 간선을 따라 갈 수 있는 길을 순서대로 나열한 것을 의미

사이클(Cycle) : 경로의 시작 정점과 마지막 정점이 같은 경로를 의미

인접 정점(adjacent vertex): 간선에 의해 직접 연결된 정점

 

그래프 구현

그래프를 구현하기 위해서는 정점에 대한 집합과 정점에 부속된 간선의 집합을 표현해야 한다. 그래프를 표현하는 방법은 순차 자료구조 방식을 이용한 2차원 배열의 인접행렬(Adjacent Matrix)방법과 연결 자료구조 방식인 연결 리스트를 사용하는 인접 리스트(Adjacent List) 방법이 있다.

 

 인접행렬(Adjacent Matrix)

그래프를 구성하는 정점에 대해서 두 정점을 연결한 간선의 유뮤를 저장하는 방법으로 정점의 수에 대한 정방 행렬을 사용한다.

출처 : https://kingpodo.tistory.com/46

하나의 정점에서 자기 자신으로의 자체 간선은 있을 수 없으므로 인접 행렬의 대각선의 값은 항상 0이다. 무방향 그래프에서는 A[a][b]와 A[b][a]값이 같이 때문에, 대각선을 기준으로 윗부분과 아랫부분이 대칭을 이룬다.

방향 그래프에서는 간선 [a, b]와 [b, a]가 서로 다른 간선이기 때문에 대칭을 이루지 않는다. 

 

n개의 정점을 가지는 그래프를 n * n 인접행렬로 표현하면 간선의 개수에 상관없이 항상 n * n개의 메모리를 사용한다. 그래프에 간선이 많은 경우에는 큰 문제가 없겠지만, 정점의 개수에 비해 간선의 개수가 적은 희소 그래프인 경우에는 인접 행렬이 희소 행렬이 되므로 메모리 낭비 문제가 발생한다.

 

 

인접 리스트(Adjacent List)

그래프를 표현하는 방법은 각 정점에 대한 인접 정점들을 연결 리스트로 만드는 것이다. 리스트의 각 노드는 정점을 저장하는 필드와 다음 인접 정점을 연결하는 링크필드로 구성한다.

출처 : https://kingpodo.tistory.com/46

 

그래프 탐색

하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하는 것을 그래프 순회 또는 그래프 탐색 이라고 한다. 그래프 탐색 방법은 깊이 우성 탐색과 너비 우선 탐색이 있다.

 

출처 : https://mini-ko.tistory.com/1

 

깊이 우선 탐색, DFS(Depth First Search) : 스택, 재귀함수 사용

깊이 우선 탐색은 시작 정점에서 한 방향으로 갈 수 있는 가장 먼 경로까지 깊이 탐색해가다가 더 이상 갈 곳이 없으면 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아와서 다른 방향의 간선으로 탐색을 계속함으로써 모든 정점을 방문하는 순회 방법이다.

 

너비 우선 탐색, BFS(Breath Frist Search) : 큐 사용

너비 우선 탐색은 시작 정점으로 부터 인접한 정점들을 모두 차례로 방문한 후, 발문했던 정점을 다시 시작점으로 하여 인접한 정점들을 차례로 방문하는 방법으로, 가까운 정점들을 먼저 방문하고 멀리 있는 정점들은 나중에 방문하는 순회 방법이다.

 

---

 

1,2회 #22

22. 다음 트리의 차수(degree)와 단말 노드(terminal node)의 수는?

2 차수:2, 단말 노드: 4

 

1,2회 #34

다음 트리를 전위 순회(preorder traversal)한 결과는?

 

 

3회 #29

다음 트리를 Preorder 운행법으로 운행할 경우 가장 먼저 탐색되는 것은?

 

3회 #40

다음 트리의 차수(degree)는?

 

4회 #24

다음 Postfix 연산식에 대한 연산결과로 옳은 것은?

34*56*+

 

4회 #32

다음 트리에 대한 INORDER 운행 결과는?

 

 

4회 #33

n 개의 노드로 구성된 무방향 그래프의 최대 간선수는?